발제자: 신주희

발제일: 2024년 11월 14일

키워드: [Time Domain] [Anomaly Detection] [Deep Learning] [Time Series Forecasting] [Time Series Augmentation]

1. Why this paper

• 학술제 연구 프로세스 관련 참고
• 데이터 증강 기법 중 가우시안 분포를 활용하여 데이터 분해 및 증강을 하기 위함
• AI 기반 트래픽 이상치 탐지를 통한 기지국 안정성 향상 주제 관련 이해 도모

2. Abstract

• 심층 신경망의 뛰어난 성능은 과적합을 피하기 위한 많은 양의 훈련 데이터에 달려 있음
• 그러나, 의료 시계열 분류 및 AIOps에서의 이상감지와 같은 현실의 시계열 응용에서는 라벨링이 제한되어 있음
• 훈련 데이터의 품질과 양을 향상시키는 효과적인 방법으로, 데이터 증강 [Data Augmentation]은 매우 중요한 역할
• 본 논문에서는 다양한 시계열 데이터 증강 방법을 체계적으로 리뷰

3. Introduction

• 컴퓨터 비전 분야의 Augmentation 기법 종류 : 컴퓨터 비전 분야에서는 다양한 데이터 증강 기법이 사용되어 모델의 성능을 향상시키고, 일반화 성능을 향상시키는데 활용됨

  A. 이동 Translation : 이미지를 수평 또는 수직으로 이동시켜서 새로운 이미지를 생성하는 기법, 이미지 내의 객체 위치 변화를 모방하고 다양성을 증가시키는데 효과적

  B. 회전 Rotation : 이미지를 일정한 각도로 회전시켜 새로운 이미지를 생성하는 기법, 회전은 이미지 각도에 대한 불변성을 학습하고, 다양한 크기의 객체를 인식하는데 도움이 됨

  C. 확대/축소 Scaling : 다양한 크기를 확대 또는 축소하여 다양한 크기의 이미지를 생성하는 기법, 크기 변화에 대한 강인한 모델을 학습하고, 다양한 크기의 객체를 인식하는데 도움이 됨

  D. 밝기 조절 Brightness Adjustment : 이미지의 밝기를 조절하여 새로운 이미지를 생성하는 기법, 밝기 변화에 대한 강인한 모델을 학습하고, 다양한 조명 조건에서의 객체 인식을 향상시키는데 사용됨

  E. 채도 조절 Saturation Adjustment : 이미지의 채도를 조절하여 다양한 색상의 이미지를 생성하는 기법, 채도 변화에 대한 강인한 모델을 학습하고, 다양한 환경에서의 객체 인식을 향상시키는데 도움이 됨

  F. 가우시안 노이즈 추가 Gaussian Noise Injection : 이미지에 가우시안 노이즈를 추가하여 새로운 이미지를 생성하는 기법, 노이즈에 강인한 모델을 학습하고, 다양한 환경에서의 객체 인식을 향상시키는데 사용

  G. 가로 뒤집기 Horizontal Flip : 이미지를 가로로 뒤집어서 새로운 이미지를 생성하는 기법, 객체의 좌우 대칭 변화를 모방하고, 데이터 다양성을 증가시키는 데 효과적

  H. 세로 뒤집기 Vertical Flip : 이미지를 세로로 뒤집어서 새로운 이미지를 생성하는 기법, 객체의 상하 대칭 변화를 모방하고, 데이터 다양성을 증가시키는데 사용됨

(1) 시계열 데이터 분석 분야의 데이터 증강

• 시계열 데이터 분석 분야에서 딥러닝을 활용한 연구 분야는 많이 이뤄지고 있음

  A. TimeSeries Forcasting

  B. TimeSeries Anamaly Detection

  C. TimeSeries Classification

• 하지만 시계열 데이터 분석 분야에서의 데이터 증강 관련 연구들은 컴퓨터 비전과 자연어 처리와 같은 분야와 달리 활발하게 이뤄지고 있지는 않음, 해당 논문에서는 시계열 데이터 분석에서의 데이터 증강 연구의 어려움을 크게 두 가지로 정리함

  A. 한계점 1 : 현존하는 데이터 증강 기법들은 시계열 데이터의 내재적 특성을 활용하지 못함

  • 일반적으로 시계열 데이터는 시간 종속성 (Temporal Dependency)이라는 특성을 가짐

  • 이미지나 언어 데이터와는 다르게 시계열 데이터는 크게 시간과 빈도 도메인으로 나눌 수 있는데, 이러한 각각의 Transformed Domain에 적합한 데이터 증강이 수행되어야 하기 때문에 다른 데이터에 비해 비교적 어려움이 있음

  B. 한계점 2 : 현존하는 데이터 증강 기법들은 Task에 의존적인 경향이 존재

  • TimeSeries Classification에 쓰인 증강 기법이, TimeSeries Anomaly Detection에는 적합하지 않을 수 있음

  • 또한, 데이터 간의 불균형이 큰 데이터와 그렇지 않은 데이터를 활용함에 있어서 다른 접근의 Data Augmentation이 필요할 수 있음

(2) 논문에서 제시하는 시계열 데이터 증강 기법의 분류

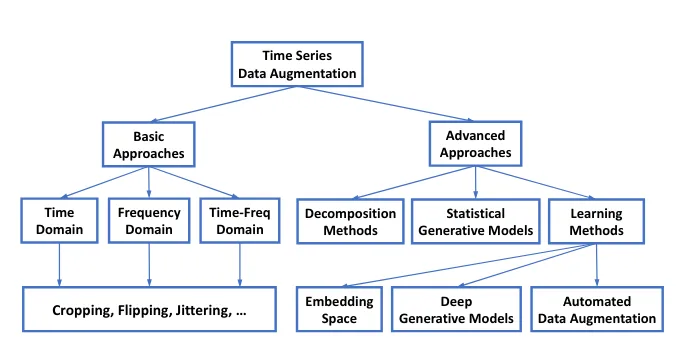
• 해당 논문에서는 시계열 데이터 증강 기법을 크게 Basic Approaches와 Advanced Approaches로 나뉠 수 있다고 제시

  • asic Approaches에서는 시간, 주파수 영역에서의 증강 기법에 대해 설명하고 Advanced Approaches에는 확률적 기법이나 학습 기법을 활용한 데이터 증강 기법에 대해 분류

(3) Basic Data Augmentation Methods

• Basic Approaches의 분류 | Time Domain | Frequency Domain | Time-Frequency Domain | | — | — | — | | Window cropping, slicing | APP (Amplitude and Phase Pertubations) | STFT (Short Fourier Transform) | | Widow warping | AAFT (Amplitude Adjusted Fourier Transform) & IAAFT (iterated AAFT) | Mel-Frequency | | Flipping | | | | Perturbation & Ensemble | | | | Noise Injection | | | | Label Expansion | | |

• Time Domain

  A. 시간 영역 변환은 시계열 데이터에 대한 가장 직관적인 데이터 증강 방법 중 하나, 대부분의 경우 이러한 방법들은 원래 입력 시계열 데이터를 직접 조작

  B. 가우시안 노이즈를 주입하거나 스파이크, 단계적 추세 및 기울기와 같은 더 복잡한 노이즈 패턴을 주입하는 것과 같은 방법

  

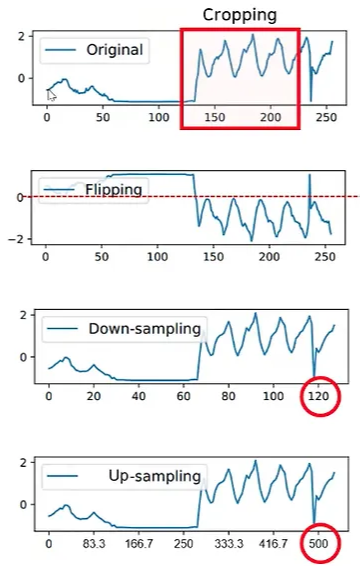
  a. Window cropping, slicing

  • Window cropping, slicing 기법은 컴퓨터 비전 영역에서의 자르기와 유사

  • 이는 원래 시계열 데이터에서 연속된 조각을 무작위로 추출하는 샘플링 방법

  b. Flipping

  • 원래 시계열을 뒤집는 방법

  c. Window warping

  • DTW (Dynamic Time Warping)와 유사한 방법으로, 원래 시계열을 compress (down-sample) 하거나 extend (up-sample) 하는 방법

  • Window warping은 원래 시계열의 총 길이를 변경하므로 딥러닝 모델에는 Window slicing과 함께 수행되어야 함

  

  d. Perturbation & Ensemble

  • Perturbation을 수행한 시계열 데이터에 대하여 DTW를 수행하여 Original data의 길이로 맞춰준 뒤 ensemble하는 DBA (DTW Barycentric Averaging) 기법을 통해 데이터를 증강하는 기법

  e. Noise Injection

  • 시계열 데이터 원본에 Noise나 Outlier를 주입하는 방법

  • Spike (계단), Step-like Trend (계단), Scope-like Trend (경사)등의 기법들이 사용되며 해당 노이즈는 Label의 정보가 변경되지 않는 매우 적은 값으로 설정해야 함

  f. Label Expansion

  • 시계열 이상치 탐지의 경우 이상치들이 단순히 한 시점이 아니라 연속적으로 길게 나타나는 특성이 있음 (Blurry)

  • 이에 단순한 시점을 이상치로 하지 않고, Label Expansion을 통해 주변까지 이상치로 정의해주는 방법

• Frequency Domain

  A. 주파수 영역은 시계열 데이터를 어떻게 주기로 표현할 수 있을까?란 질문으로 시작, 시계열 데이터를 얼마만큼의 크기로 (진폭) 어느 위치에서 출발 (위상) 할지에 대해 나눠서 확인 가능

  • Amplitude Spectrum : 시계열 데이터가 갖는 주파수 성분들의 진폭

  • Phase Spectrum : 각 주파수 성분들의 시간 축 상의 위치를 의미함

    

  B. Fourier Transform 푸리에 변환

  b1. 일반적으로 시계열 데이터는 여러 종류의 Sin, Cos 파장들로 이루어져 있음

  b2. 푸리에 변환은 신호의 주파수 분석을 수행할 때 사용되며, time Domain을 Frequency Domain으로 변환해줌

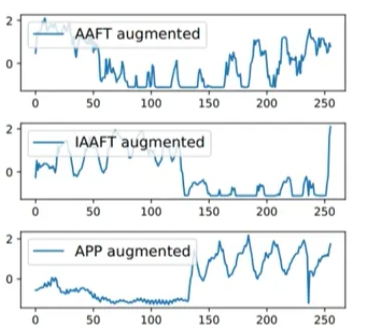
  • APP (Amplitude and Phase Perturbations)
    • 앞서 소개했던 시계열 데이터의 Amplitude Spectrum과 Phase spectrum에 Perturbation을 수행한 기법
    • Amplitude Spectrum은 일부 데이터를 원본 데이터의 평균과 분산을 갖는 Gaussian Noise로 대체하고 Phase Spectrum은 일부 데이터에 zero-mean Gaussian Noise를 더함
  • AFT (Amplitude Adjusted Fourier Transform) & IAAFT (Iterated AAFT)

  

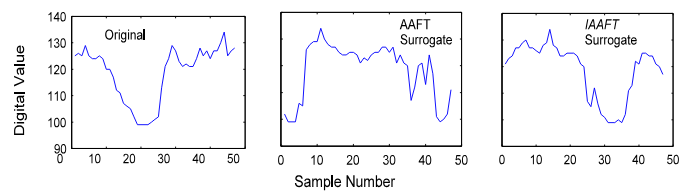
  • AAFT는 푸리에 변환 후 Phase Spectrum에서 무작위로 Phase를 Shuffle한 뒤 Inverse Fourier Transform을 수애하여 Amplitude는 보존되고 Phase만 바뀐 데이터를 생성하는 기법
    • IAAFT는 AAFT의 발전된 버전으로, iterative step을 통해 AAFT가 좀 더 잘 수렴할 수 있도록 개선시킨 방법
    • AAFT와 IAAF 기법의 장점은 해당 기법들로 생성된 시계열 데이터는 대략적으로 기존 시계열 데이터의 시간 상관 관계, 전력 스펙트럼 및 진폭 분포 보존이 가능하다는 것

  c. Time-Frequency Domain

  

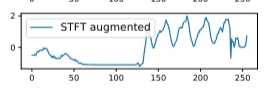
  • STFT (Short Fourier Transform)
    • STFT는 주파수 특성이 시간에 따라 달라지는 특징을 분석하기 위한 방법
    • 즉, 시계열 데이터를 시간 단위로 짧게 분할한 뒤 FFT를 수행하는 방법
  • Mel Spectrogram
    • 주파수의 단위를 특정 공식에 맞춰 멜 단위 (Mel unit)으로 변경한 스펙트럼
    • 청각이 저음의 주파수 변화에 민감하고 고음의 주파수 변화에 덜 민감한 특징을 사용하여 만들어진 기법

(4) Basic Data Augmentation Methods

• Advanced Approaches의 분류

  A. Decomposition

  • Seasonal-Trend Decomposition Algorithm for Long Time Series (STL)
  • Robust STL
  • Bootstrap STL

  B. Statistical

  • Mixture of Gaussian Trees
  • LGT (Local and Global Trend)
  • Mixture of AR (MAR) models (AR : AutoRegressive)

  C. Deep Learning

  • Embedding Space
  • Deep Generative Models
  • Automated Data Augmentation

• Decomposition

  

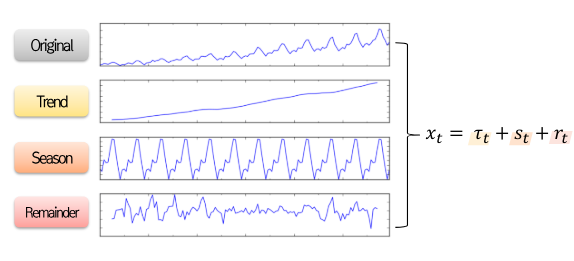
  • Decomposition 기법은 시계열 데이터를 Trend, Season, Remainder로 분해하는 STL 기법을 활용한 증강 기법

  A. Seasonal-Trend Decomposition Algorithm for Long Time Series (STL)

  B. Robust STL

  • STL을 통해 Trend, Season, Remainder를 분해한 다음 가중치를 조절하여 데이터를 생성 가능

  C. Bootstrap STL

  • STL을 거치면서 생긴 Remainder에 BootStrap을 적용하여 데이터를 증강하는 기법으로 Bootstrapping을 적용하여 증강 데이터를 생성한 다음 Trend와 Season을 다시 추가하여 새로운 데이터 생성

• Statistical Generative Model

  A. Statistical Generative model은 시계열 데이터의 conditional distribution을 반영한 데이터 증강 기법으로 t 시점에서의 증강 기법을 통해 생성된 데이터는 이전 포인트의 영향을 받는다고 가정하는 것으로 시작

  • Mixture of Gaussian Trees
    • Mixture of Gaussian trees를 활용하여 멀티 모달 환경에서의 소수 클래스를 오버 샘플링하여 데이터 불균형 분류 문제를 해결하려고 함
    • 이는 TimeSeries correlations between neighboring points를 고려하여 모델링하였다는 점에서 기존 오버 샘플링 기법과 차이가 있음
  • LGT (Local and Global Trend)
    • 통계 알고리즘으로써 계산된 해당 알고리즘으로 계산된 매개변수 및 예측 경로의 표본을 사용
  • Mixture of AR (MAR) models (AR : AutoRegressive)
    • MAR 모델을 활용하여 시계열 집합을 시뮬레이션하고 시계열 Feature space에서 생성된 시계열의 다양성과 적용범위를 조사

• Deep Learning method

  A. Embedding Space

  

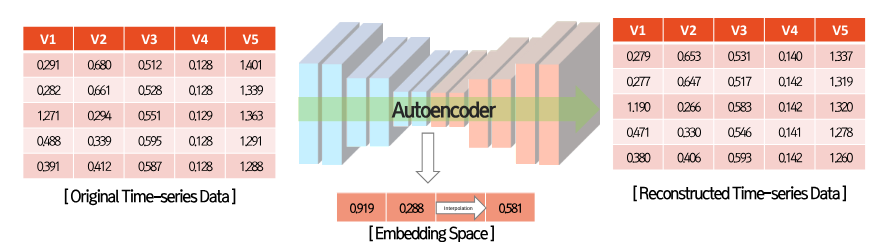
  • Embedding Space 기법은 데이터 증강을 학습된 Embedding Space로부터 수행할 수 있다는 연구
    • Raw input에 대한 데이터 증강보다 embedded input에 대한 데이터 증강이 효과적임을 주장하는 방법
    • Sequence AutoEncoder을 통해 Encoder를 학습하고, Encoder의 입력에 조금 변형된 데이터를 넣고 데이터 증강을 수행

  B. Deep Generative Models

  • Generative Adversarial Network (GAN)과 RNN을 결합한 모델인 RGAN과 RCGAN을 활용하여 데이터르 증강하는 기법, 이미지 생성에 주로 사용되는 Deep Generative Models (DGM)을 시계열 데이터 생성에 적용한 사례로써 Recurrent GAN (RGAN)과 TimeGAN 두 알고리즘이 대표적
    • RGAN : 실제 시계열 데이터의 시퀀스와 유사한 데이터를 생성
    • RCGAN : 일부 조건부 입력에 따라 실제 시계열 데이터의 시퀀스와 유사한 데이터를 생성

(5) Preliminary Evaluation

• Time Series Classification

  • 데이터 증강의 유무에 따른 분류 성능 비교

  • Alibaba Cloud Monitoring System에서는 이진 클래스 레이블로 5분 간격의 1주 길이 시계열 5000개를 수집함

  • 이를 무작위로 전체 샘플의 80%와 테스트 세트로 나누어 적용된 데이터 증강 방법이 크로핑, 워핑, 플리핑이며, 아웃라이어 주입 시 데이터 증강이 정확도를 0.1%에서 1.9% 향상 시킨 것을 확인

• Time Series Anomaly Detection

  • 시계열 이상 탐지에서 데이터 부족과 불균형 문제를 해결하기 위해 데이터 증강을 통해 더 많은 레이블 데이터 생성 권장

  • 데이터 증강이 적용된 U-Net-DeWA의 데이터 증강 방법은 플리핑, 크로핑, 레이블 확장, 주파수 도메인에서의 APP 기반 증강 등이 포함

  • 분해가 F1 점수를 향상시키, 데이터 증가이 성능을 더욱 높임

• Time Series Forecasting

  • DeepAR와 Transformer에서 데이터 증강의 실질적인 효과를 보여줌

  • 크로핑, 워핑, 플리핑 및 주파수 도메인에서의 APP 기반 증강과 같은 기본 증강 바법을 고려

  • 데이터 증강 방법이 모든 모델에서 평균적으로 긍정적인 결과를 가져오는 것을 확인했지만, 특정 데이터/모델 조합에서는 부정적인 결과도 관찰

  • 향후 연구로는 시계열 예측에 맞는 데이터 증강 정책을 자동으로 탐색하여 데이터 증강의 영향을 안정화하는 방안을 모색할 필요성 제기

(6) Discussion for Future Opportunities

• Augmentation in Time-Frequency Domain

  • 시계열 데이터 증강의 시간-주파수 도메인에서는 STFT 기반의 연구가 제한적이며, 웨이브렛 변환과 그 변형들이 비정상 시계열과 비가우시안 노이즈를 효과적으로 처리할 수 있는 방법

  • 최대 중첩 이산 웨이브렛 변환(MODWT)은 계산 효율성, 다양한 시계열 길이 처리 가능성, 더 높은 해상도를 제공하여 시계열 분석에 유리

• Augmentation for Imbalanced Class

  • 시계열 분류에서 클래스 불균형 문제는 흔히 발생하며, 이를 해결하기 위한 접근법인 SMOTE는 소수 클래스의 과표집을 통해 불균형을 완화하지만, 데이터 분포를 변경하고 과적합을 유발할 수 있음

  • 또 다른 방법으로는 비용 민감 모델을 설계하여 손실 함수를 조정하고, 클래스 레이블과 샘플 이웃에 대한 가중치를 고려하는 기법이 있음

• Augmentation Selection and Combination

  • 데이터 증강 방법의 조합과 선택 전략이 중요하며, 여러 연구에서 다양한 시간 도메인 증강 방법을 결합할 때 성능 향상이 나타남

  • 여러 증강 방법을 직접 결합하면 데이터 양이 방대해지고 효율성이 떨어질 수 있음

  • RandAugment는 이미지 분류와 객체 탐지에서 증강 방법을 효율적으로 조합하는 방법으로, 향후 시계열 데이터에 적합한 증강 선택 및 조합 전략을 설계하는 것이 흥미로운 연구 방향일 수 있음

• Augmentation with Gaussian Processes

  • 가우시안 프로세스(GPs)는 시계열 분석에 적합한 베이지안 비모수 모델로, 함수 공간 관점에서 함수에 대한 분포를 유도

  • GPs는 평균 함수와 공분산 커널 함수로 특징 지어지며, 커널의 선택에 따라 모델링하는 함수의 일반적인 속성(매끄러움, 주기성 등)을 가정

  • 심층 가우시안 프로세스(DGPs)는 GPs의 계층적 조합으로 더 풍부한 모델을 제공하지만 시계열에 대한 연구는 부족

• Augmentation with Deep Generative Models

  • 현재 시계열 데이터 증강에 주로 사용되는 딥 생성 모델(DGMs)은 GANs이지만, 다른 모델들도 큰 잠재력을 가짐

  • 예를 들어, 딥 자가 회귀 네트워크(DARNs)와 정규화 흐름(NFs), 변량 오토인코더(VAEs) 등이 시계열 데이터 생성 및 모델링에 유망한 성능을 보여줌

4. Conclusion

• 본 논문에서는 딥러닝 모델이 시계열 데이터에서 점점 더 인기를 끄고 있으므로, 제한된 레이블 데이터는 효과적인 데이터 증강 방법의 필요성을 강조
• 높은 성능 향상을 가져온 이미지, 자연어, 스피치 등에 적합한 증강 기법은 시계열 데이터에 적용하기 어려우며, 기존 연구에 Basic Approches와 Advanced Approaches를 적용해볼 필요

5. Take away

• 시계열 데이터만을 위한 데이터 증강 기법의 필요성은 대두되고 있음
• 높은 성능 향상을 가져온 이미지, 자연어, 스피치 등에 적합한 증강 기법은 시계열 데이터에 적용하기 어려우며, 기존 연구에 Basic Approches와 Advanced Approaches를 적용해볼 필요가 있음을 기억
• 시계열 데이터의 증강 기법은 아직 까지도 많은 연구가 진행 중이고, 복잡한 task이므로 추가적인 공부가 필요