발제자: 권재빈

발제일: 2025년 01월 18일

키워드: [Data Augmentation] [Traditional algorithms] [VAE] [GANs] [Deep Learning] [Machine Learning]

1. Why this paper

• 시리얼 데이터에서 데이터 증강을 위한 관련 지식 필요
• 다양한 생성형 모델에 대한 지식 필요
• 동계학회 포스터 발표 예정

2. Summary of Paper

Abstract

• 최근 딥러닝 기반 생성 모델(Deep Learnig-based generative models)의 발전은 시계열 데이터 처리에 뛰어난 성능을 보임. 하지만, Deep Neural Networks는 시계열 데이터 작업에 있어서 훈련 데이터셋의 크기와 일관성에 의존하는데, 현실 세계에서는 데이터셋이 제한적이고 보안과 같은 제약조건으로 인해 데이터 부족 문제가 발생함.

• 이러한 문제를 해결하기 위해 데이터 증강 기법(Data Augmentation techniques)이 소개됨. 데이터 증강 기법은 기존 데이터에 노이즈 추가(Adding Noise), 데이터 순열(Permutations), 그리고 합성 데이터 생성(Synthetic Data Generation) 방법을 통해 데이터를 풍부하게 하여 모델의 성능을 향상시킬 수 있음.

• 이 논문을 통해 시계열 데이터 증강 기법의 최신 동향을 검토하고 알고리즘을 분류함으로써 연구자들에게 가이드를 제공하고자 함

1. Introduction

• 딥러닝(DL)에서 Supervised Learning이 주로 사용되는데, Supervised Learning은 학습에 labeling된 많은 데이터가 필요하지만 이에 적합한 데이터셋을 찾기 점점 더 어려워지고 있음. 특히 시간 시계열 데이터에서는 프라이버시와 같은 문제들로 인해 데이터셋 접근이 어려워 충분한 크기의 균형잡힌 데이터를 가지는 데이터셋을 얻는 것이 어려움.

• 일반적으로, 이러한 문제를 해결하기 위해 Subsampling과 같은 전처리 기법이 사용되거나, 데이터셋의 크기가 충분히 크지 않은 경우 DA 기법(Data Augmentation techniques)이 사용됨.

• Artificial Neural Networks(ANNs)와 이를 DL 분야에 적용하는 것이 발전을 이룸에 따라 다양한 생성형 모델이 DA에 제안되었음. 대표적으로 Autoencoder(AE), Variational Autoencoder(VAE), Generative Adversarial Networks(GANs)를 활용하여 DA를 수행함. 이를 통해 machine learning에 사용되는 데이터 세트의 크기를 늘릴 수 있음.

• 시간 시계열 데이터는 시간 종속성(Time Dependency)와 패턴 보존이 중요한 특성을 가지므로 데이터를 가공할 때 다른 데이터에 비해 더 많은 주의가 필요함.

-따라서, 이 논문을 통해 현존하는 DA 기술을 검토하고 각각의 긍정적인 측면과 부정적인 측면을 분석하고자 함.

2. Problem Statement

• 이 논문의 목적은 시간 시계열 데이터의 DA에서의 다양한 접근 방식이 어떻게 개발되었는지와 업데이트된 최신기술에 대한 포괄적인 연구를 제공하고자 함.

3. Related Works

• 최근 DA 분야 리뷰 논문들은 주로 이미지, 비디오, 자연어 처리와 같은 분야에 초점을 맞추고 있어 시간 시계열 데이터의 경우 데이터 불균형과 부족 문제가 심각하지만, 이에 대한 연구는 제한적임.

• 시계열 데이터셋의 품질을 향상시키기 위해 새로운 기술의 등장에도 불구하고, 특정 기술이나 모델에 집중하는 연구는 존재하지만, 종합적으로 비교하고 분석하는 연구는 부족함. 따라서, 이 논문을 통해 시계열 데이터의 DA 기술을 포과적으로 검토하고 비교 분석을 진행하여 실질적인 가이드를 제공하고자 함.

4. Background

4.1 Traditional algorithms

• 데이터가 불균형하거나 부족할 때, DA는 이를 해결하기 위한 중요한 작업으로 활용됨. 이미지 인식 분야에서 cropping, scaling, mirroring, color augmentation, translation 등의 기법이 사용됨.

• 하지만, 이러한 이미지 데이터 증강에서 사용되는 많은 기법들은 시계열 데이터에는 직접적으로 적용될 수 없음. 또한, 시계열 데이터의 다양성으로 인해 특정 데이터셋에 적합한 기술이 다르므로 각 데이터셋에 적합하도록 알고리즘을 수정하거나 새로운 알고리즘을 설계해야 함.

• Traditional algorithms은 데이터 입력 샘플을 취하고 이러한 데이터를 수정하고 다른 변환을 적용하여 새로운 샘플을 합성하는 모든 기술로 정의됨.

4.2 Variational Autoencoder(VAE)

• VAE는 Autoencoder(AE) 구조를 기반으로 발전된 모델로, AE는 입력 데이터를 받아 약간의 변형을 통해 출력을 생성하는 self-supervised training 방식으로 동작함.

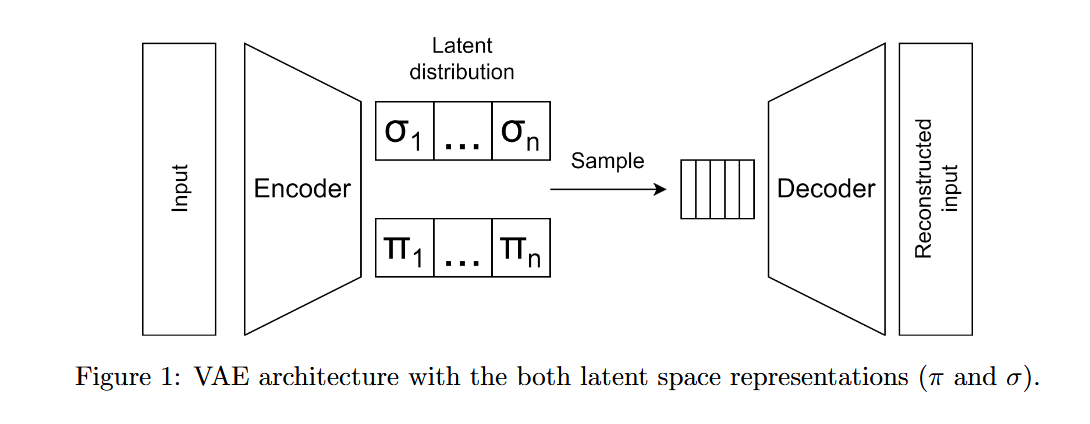
• AE의 구조: Encoder와 Decoder로 구성되어 있으며, Encoder는 입력 데이터를 낮은 차원의 latent space로 압축하고 Decoder는 압축된 latent space에서의 값을 보간하여 원본 데이터와 유사한 합성 데이터(출력 데이터)를 생성함. 그러나 이러한 보간은 완전히 새로운 값을 생성하는 것이 아니라 학습된 확률 분포의 feature들을 혼합한 것으로 한계가 존재함.

• VAE의 구조: AE와 동일한 구조를 가지지만, encoding 과정에서 latent space로 특정 point가 아닌 확률 분포로 encoding을 수행하고 decoder에서 이러한 latent space에서의 평균과 표준편차를 통해 sampling하여 decoding을 수행함으로써 합성 데이터를 생성함.

• VAE의 loss fuction은 reconstruction term과 regularisation term으로 두 가지 항의 합으로 구성됨. reconstruction term: 입력 데이터를 복원할 때 발생하는 오류를 측정하는 것으로 출력 데이터와 입력 데이터 간 차이를 최소화하도록 함. regularisation term: KL Divergence를 사용하여 latent space에서 sampling된 데이터와 가우시안 분포 간의 거리(유사도)를 측정하여 샘플링된 point들이 정규 분포를 따르도록 유도함.

4.3 Generative Adversarial Networks(GANs)

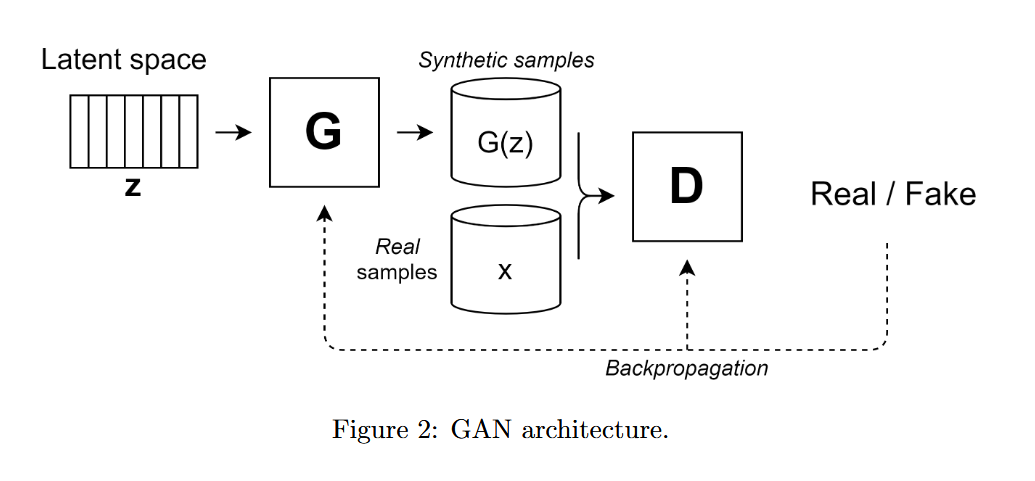
• GAN의 구조: 입력으로 latent vector z를 받아 synthesied samples(fake samples)를 생성하는 Generator와 입력 데이터를 real sample인지 fake sample인지를 구분하는 Discriminator로 구성됨.

• GAN의 동작원리: Generator는 Discriminator를 속이기 위해 더욱 real data와 구분되지 않는 fake data를 만들고자 하고 Discriminator는 이를 더 잘 구분하고자 하여 서로 경쟁하며 학습함. 이 때, Discriminator가 데이터를 정확히 구분하면 Generator에 negative feedback을 보내고 데이터를 구분하지 못하면 Generator는 positive feedback을 받음. 이를 수학적으로 objective fuction을 정의하면 다음과 같은 minmax fuction과 같다.

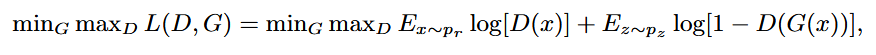
이 때, 수식의 의미는 real data x와 fake data G(x)를 잘 판단하는 discriminator(D)를 선택하고 이에 대해 fake data와 real data를 잘 구분하지 못하도록 하는 Generator(G) 선택한다는 의미를 가짐.

• GAN은 이론적으로 loss를 더 이상 줄일 수 없는 상태인 Nash Equilibrium에 수렴할 수 있지만, 실제로는 GAN의 학습 과정에서의 불안정성으로 인해 도달하기 어려움.

• GAN은 원본 데이터의 분포를 학습하여 새로운 데이터를 기반으로 데이터를 생성하기 때문에 원본 데이터를 변형하여 새로운 데이터를 생성하는 기존의 다른 DA 기법보다 다양한 sample들을 생성 가능함.

5. Evaluation metrics

• 시간 시계열 데이터의 특수성으로 인해 모든 application에 통용되는 유일한 평가 지표는 존재하지 않음. 데이터의 품질과 다양성을 평가할 수 있는 적합한 측정 방법은 계속해서 연구 중임.

5.1 External performance evaluation

• 대부분의 traditional alogoritms은 DA 적용 전후의 모델 성능을 비교하여 새로운 데이터가 모델에 미친 영향을 측정하는 방법을 사용함.

• [32]에서는 symmetric Mean Absolute Percentage Error와 Mean Absolute Scaled Error를 사용해 DA 적용 전후를 비교함.

• [15]에서는 VGG[24], Residual Network[25], Multilayer Perceptron[33], Long ShortTerm Memory[34], Bidirectional Long Short-Term Memory[35], Long Short-Term Memory Fully Convolutional Network[36]의 6가지 신경망을 사용해 DA 알고리즘이 모델 분류 정확도에 미치는 영향을 비교함. 그 결과, 각 아키텍처마다 고유한 특성이 있어 각 알고리즘마다 결과가 다르게 나타나 최상의 알고리즘을 구별하기가 어려움. 추가로, 모두 신경모델이기 때문에 일부 결과의 해석이 어려움.

• [29]에서는 각 연구 사례에서 연구된 정확도의 증가를 통해 다양한 DA 기술을 비교함. Noise Addition, GAN, Sliding Window, Fourier-Transform and Recombination of Segmentation와 같은 서로 다른 기술들을 특정 도메인의 목적에 맞춰 비교함.

• GAN architecture는 동일한 loss fuction을 사용해 네트워크 간의 성능을 비교함. 이 때, 합성 데이터의 품질과 loss fuction은 상관성을 가짐. 하지만, 이 방법은 신경망 모델에 한정된 평가 방법으로 다른 모델에는 적용이 어렵고 데이터 자체의 품질이 아닌 모델 성능 개선에 포커스를 두고 있다는 단점이 존재함.

• [41]에서는 Mean Per-Class Error(MPCE)를 통해 DA 기술의 성능을 비교함. MPCE는 클래스 별 error rate을 측정하여 여러 데이터셋에서 성능을 평가함.

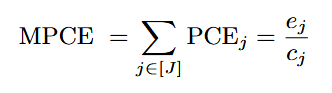ej는 해당 데이터셋에서의 error rate을 의미하고 cj 각 데이터셋의 클래스 수를 의미함.

5.2 GAN related metrics

• GAN이 생성한 합성 데이터의 quality와 diversity를 측정하는 것은 여전히 해결되지 않은 과제임. 특히, 대부분의 측정 방법의 연구는 computer vision 분야에 집중되어 있어 이를 시계열 데이터에서 알맞게 적용하는 것이 어려움.

• GAN이 생성한 시계열 데이터의 성능을 측정하는 방법

  1. 시계열 데이터를 image 데이터로 취급하여 컴퓨터 비전에서 설계된 전통적인 평가 지표(Inception Score, Mode Score, Frechet Inception Distance)를 적용함.
  2. 시계열 데이터에 특화된 평가 지표를 설계하여 시계열 데이터의 성능을 직접적으로 평가함. 이 때, Discriminative Score는 외부에서 사전 학습된 2-layer Long-Short Term Memory(LSTM) 모델을 사용해 real data와 fake data를 구분하여 classification error를 계산함. 반면에, Predictive Score는 synthetic data를 통해 모델을 학습한 후 real data로 Mean Absolute Error(MAE)를 측정하여 평가를 진행함. 현재, 이 방법이 시계열 데이터의 성능을 평가할 때, 가장 효율적이고 자주 사용됨.

5.3 Similarity measurements

• Similarity measurements는 original data와 DA를 통해 생성된 synthetic data의 확률 분포가 얼마나 차이 나는지 측정을 통해 성능을 평가함. 이는 앞의 방법에서와 다르게 데이터의 quality를 직접적으로 평가 가능하고 알고리즘에 상관없이 모든 synthetic data에 적용할 수 있다는 장점을 가짐.

• 두 분포 간의 차이를 측정하는 실증적, 정성적 접근 방식은 데이터의 차원을 줄이고 시각적 비교를 수행하는 것임. [57]에서는 t-distributed Stochastic Neighbour Embedding (t-SNE)와 Principal Component Analysis (PCA)를 통해 data를 2D 공간으로 차원을 축소하고 TimeGAN, Recurrent Conditional GAN, Continuous recurrent GAN, T-Forcing, WaveNet, WaveGAN의 분포를 original data의 분포와 비교하여 성능을 측정함.

• 데이터의 분포 차이를 측정하는 방법 KL Divergence: 두 확률 분포 P와 Q 간의 거리(유사도) 측정함. P Q 순서를 바꾸면 결과값이 바뀌기 때문에 비대칭적임. 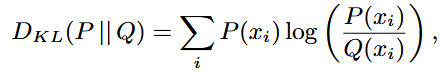Jensen-Shannon Divergence(JSD): KL Divergence를 변형하여 대칭적으로 두 분포 사의의 관계를 측정함. 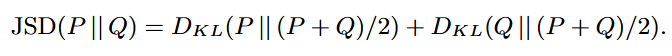Wasserstein-Fourier distance: 시간 시계열 데이터의 분포를 비교하기 위해 제안된 것으로 power spectral density의 Wasserstein distance를 계산하여 real data와 synthetic data의 분포를 비교함. 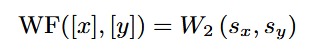이 때 Sx와 Sy는 정규화된 power spectral density를 의미함.

6. Data Augmentation algorithms review

• 이 섹션을 통해 다양한 최신 DA 알고리즘을 검토하고 각 알고리즘의 특수성과 강점 그리고 약점을 분석하고자 함. 또한 다양한 DA 알고리즘 간의 관계를 분석하여 그룹화된 관계를 살펴보고자 함.

6.1 Basic DA Methods

• 기존 데이터를 변형, 축소, 확대, 수정하여 새로운 데이터 샘플을 생성하는 방법으로 전통적으로 컴퓨터 비전 분야에 사용됨. 이러한 일부 알고리즘은 시계열 데이터에 적용 가능하지만, 새로운 알고리즘이 필요한 경우도 존재함.

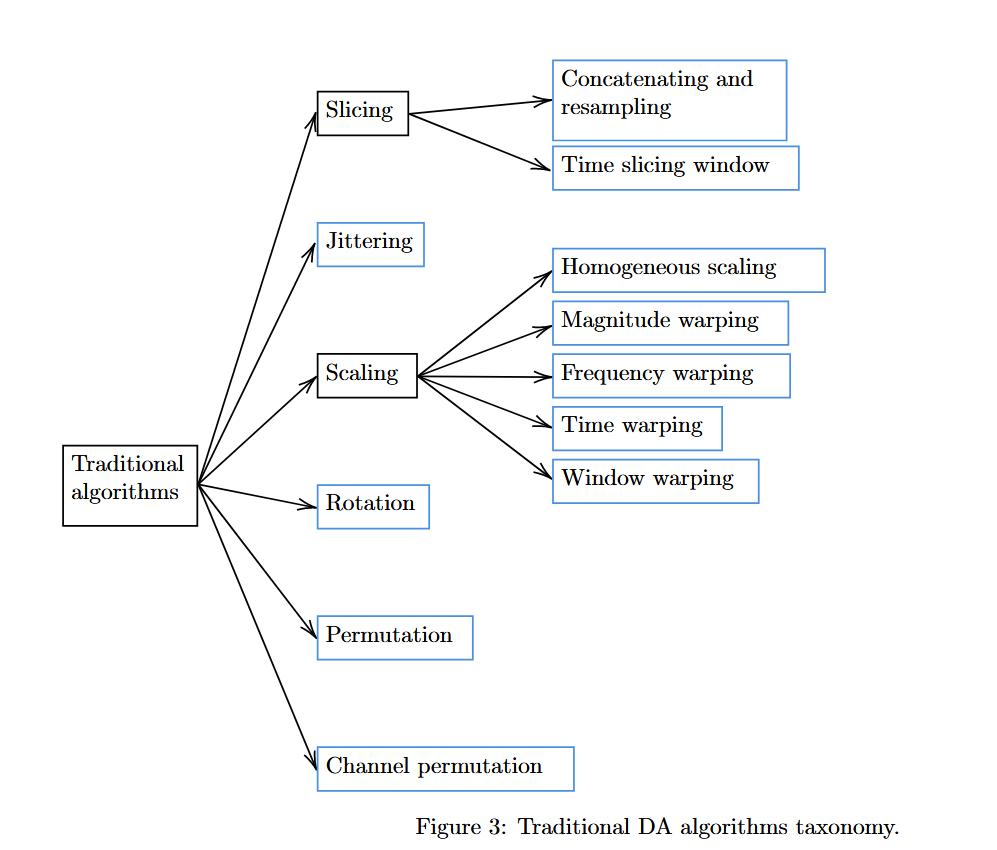
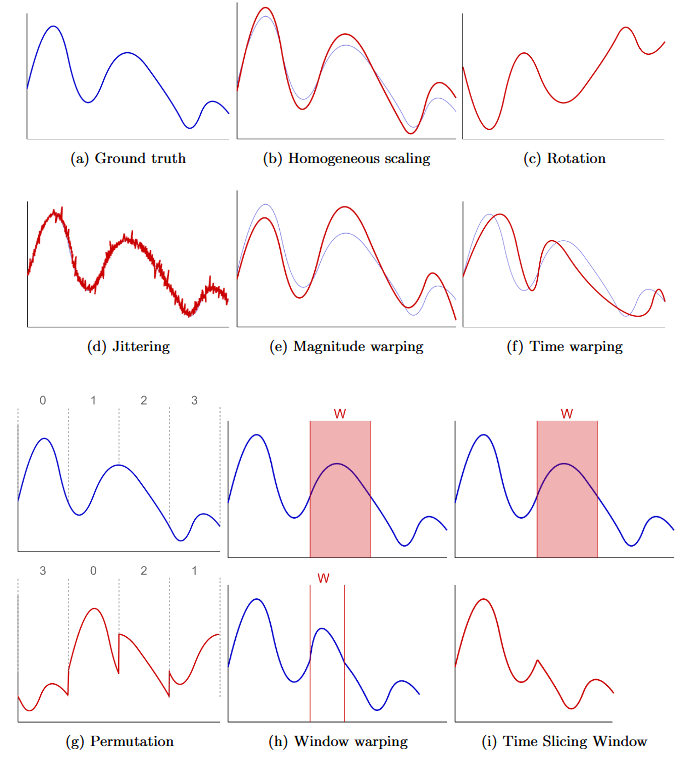
6.1.1 Time slicing window

• 시간 시계열 데이터를 끝부분 또는 임의의 구간을 일정 부분 잘라내어 새로운 샘플을 생성하는 방법으로 슬라이싱된 데이터는 다음과 같이 정의함. 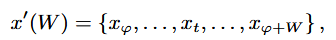이 때, W는 슬라이스 윈도우의 크기를 나타내고 φ는 슬라이스 시작점을 나타냄. 이 방법은 원본 데이터의 중요한 feature을 잘라낼 수 있기 때문에 유효하지 않은 합성 데이터를 생성할 수 있음.

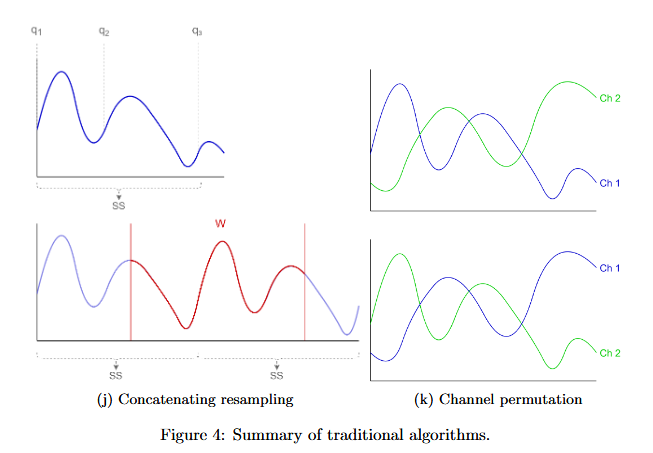
• Concateneating and Resampling Method: 앞의 slicing의 문제를 해결하기 위해 제안된 방법. 먼저 Pan-Tompkins QRS detector를 사용하여 데이터의 feature인 characteristic points들을 뽑아낸 후, 이러한 characteristic points를 기준으로 시작점과 끝점을 정의하여 subsequence를 만들어 이를 여러 번 복제하고 슬라이싱하여 DA를 수행함. 이를 통해 신호의 중요한 feature들을 유지하여 synthetic data의 유효성을 보장할 수 있지만, characteristic points를 검출할 수 있는 검출기가 필요하다는 한계가 존재함.

6.1.2 Jittering

• Jittering은 시간 시계열 데이터에 노이즈를 추가하여 DA를 수행하는 방법으로, 간단하며 가장 널리 사용되는 DA 기법 중 하나임. 데이터가 기본적으로 노이즈를 포함한다고 가정하고, 이를 활용해 새로운 샘플을 생성하는데 일반적으로 Gaussian Noise가 각 시간 단계에 추가됨.

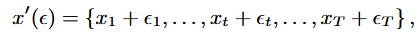
ε은 각 신호 단계에 추가된 노이즈를 의미하고, 평균과 표준편차를 통해 노이즈의 크기와 변형 정도가 결정됨. 따라서, 노이즈의 특성은 application에 따라 다르게 설정함.

• [70]에서와 같이 noise가 부적절하게 추가될 경우 학습 성능에 부정적인 영향을 미칠 수 있으므로 반드시 각 경우에 맞게 process를 조정해야 함.

6.1.3 Scaling

• 시간 시계열 데이터의 특정 구간의 크기를 조정하여 새로운 데이터를 생성하는 방법으로 신호의 전반적인 형태는 유지하면서 값의 범위를 변경함. 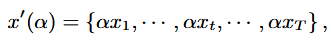여기서, α는 0보다 큰 값으로 크기 조정을 해주는 scale 값으로, 주로 평균이 1이고 표준편차를 hyperparameter로 설정하여 가우시안 분포에서 추출함.

• Magnitude Warping: 데이터 곡선에 특정 지점에 따라 가변적인 크기 조정을 수행하는 방법. 구체적으로는, 먼저 knots를 통해 크기 조정을 적용할 지점을 정의하고 정규분포를 활용하여 구간 크기를 정함. 다음으로, cubic spline interpolation을 통해 scaling 크기를 정의하여 synthetic data를 생성함. 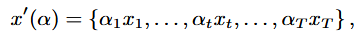이 방법의 특징은 곡선의 전반적인 형태를 유지하며 다양한 변형이 가능하다는 점으로 변형 후에도 synthetic data는 유효성을 유지한다고 가정함.

• Frequency Warping: 주로 음성 신호 처리에서 사용되는 방법으로, 신호의 주파수 영역에서 변형을 수행함. 음성 인식에서 가장 널리 사용되는 버전은 Vocal Tract Length Perturbation으로, 이는 결정론적 방식 또는 특정 범위 내에서 확률론적으로 적용 가능함.

• Time Warping: 시간 축을 조정하여 신호의 특정 구간을 늘리거나 줄이는 방식으로 Magnitude Warping과 마찬가지로 cubic spline interpolation을 사용하여 knots를 기준으로 매끄러운 곡선을 생성함. 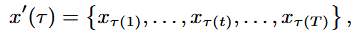이 때, τ는 시간이 왜곡되는 정도(magnitude)를 의미함.

• Window Warping: 시간 시계열 데이터의 특정 슬라이스에 대해 속도를 1/2배로 줄이거나 2배로 늘림을 통해 synthetic data를 생성하는 방법. 이 때, 변형되는 슬라이스를 제외하고 나머지 구간은 변형되지 않음.

6.1.4 Rotation

• Multivariate time series data 에서는 rotation matrix를 적용하여 데이터를 회전하고, Univariate time series data에서는 데이터를 flipping(반전)하여 회전을 적용하여 synthetic data를 생성하는 방법.

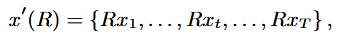
• Rotation 방법은 시계열에서는 그리 유용하지 않은데, 시계열 데이터를 회전하면 클래스 정보가 손실될 위험이 존재하기 때문임. 반면에, 다른 데이터 변환 기법과 결합하여 사용하면 데이터의 다양성이 증가하여 유용하게 사용 가능함.

6.1.5 Permutation

• 시계열 데이터를 window 조각으로 나누고, 이를 섞어서 새로운 데이터를 생성하는 방법으로, 이 때 window size는 고정되어 있을 수도 있고 변할 수도 있음. 이 방법은 slice들을 임의로 재배열하기 때문에 time dependencies를 잃어버려 유효하지 않은 샘플을 생성할 수 있음. 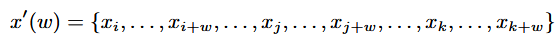이 때, i, j, k는 각 window의 첫 번째 인덱스 슬라이스를 나타내고, w는 window size를 의미함.

6.1.6 Channel permutation

• multi-dimensional data에서 서로 다른 channel의 위치를 변경하여 DA를 수행하는 방법. 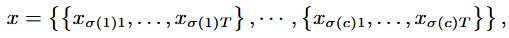c는 채널의 수를 나타내고, σ는 채널의 순서를 결정하는 함수임.

• 시간 시계열 데이터에서 이 알고리즘을 적용하기 위해서는 채널 정보와 특정 채널이 독립적인 경우를 가정해야 적용 가능함. 그 사례로는, [63]에서 8개의 센서를 사용한 운동 매트 데이터를 분석할 때 센서 위치를 바꾸는 방식으로 채널 위치를 변경하여 새로운 데이터를 생성함.

6.1.7

6.2 Data Augmentation through VAE

• VAE는 AE의 발전된 형태로, 데이터의 편차를 더 정밀하게 제어하여 더 좋은 synthetic data를 생성 가능하게 함.

• LSTM을 사용하여, [81]에서 VAE를 통해 이상치 탐지 문제를 위한 데이터를 생성하였고, [82]에서는 인간 활동 인식을 위해 VAE로 증강된 데이터셋을 사용해 모델 성능을 개선함. [83], [84]에서는 데이터셋의 크기를 늘리는 데 있어 이러한 알고리즘의 효율성을 보여줌.

• [85]에 따르면, VAE가 신경망 모델뿐만 아니라 전통적인 머신러닝 알고리즘에서도 성능 향상이 가능함. 또한, 비지도 학습에서도 활용 가능함[86]. 마지막으로, VAE, AE, WGAN-GP를 결합해 시계열 데이터 증강에 활용하는 연구도 존재함[87].

• classification, forecasting, value imputation, value prediction와 같은 생성된 데이터가 사용되는 문제의 특성에 따라 모델 간의 차이가 발생함.

6.2.1 Taxonomy for the VAE algorithms reviewed

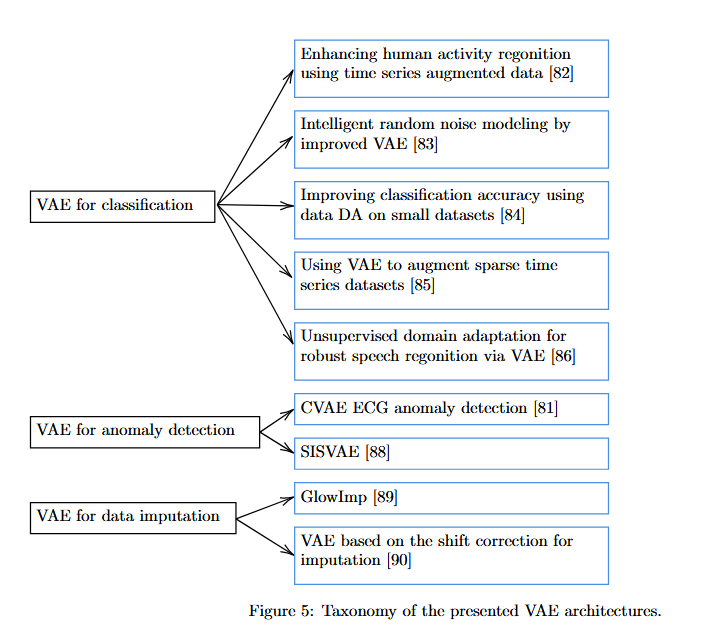
6.2.2 VAEs for anomaly detection

• VAE는 이상치 탐지에서 부족한 데이터 샘플을 생성하여 데이터셋을 보완하는 데 활용됨. 이를 통해 머신러닝 모델 학습 과정에서의 데이터 부족 문제를 해결함.

• CVAE ECG anomaly detection[81]: 심장 장애를 나타내는 ECG 신호와 정상 신호를 분류하기 위해 10초간 3600 sample에서 downsampling한 905 sample을 사용함. CVAE는 ECG 신호의 데이터를 처리하는 LSTM layer로 구성되어 정상 샘플과 이상 샘플의 분류를 학습함.

• SISVAE[88]: 시간적 종속성을 유지하기 위해 순환 레이어가 있는 VAE를 사용함. time step 간의 급격한 변화를 방지하기 위해 KL Divergence를 사용하여 연속적인 시간 단계 간의 보정 편향을 계산하여 적용함.

6.2.3 VAEs for data imputation

• data imputation은 missing data가 존재하는 샘플에서 새로운 데이터를 생성하여 빈 공간을 채우는 작업을 수행함. 시간 시계열 데이터에서는 원본 데이터 분포를 기반으로 missing data를 채움.

• GlowImp architecture[89]: Glow VAE와 Wasserstein GAN 부분으로 구성됨. Glow VAE는 기존 VAE의 encoder의 latent distribution을 취하고, Glow Model을 통해 missing values를 보간하는 기능을 함. GAN 부분은 VAE의 decoder를 생성기로 하여, discriminator를 통해 real/fake data를 구분하여 현실적인 샘플을 생성하도록 유도함.

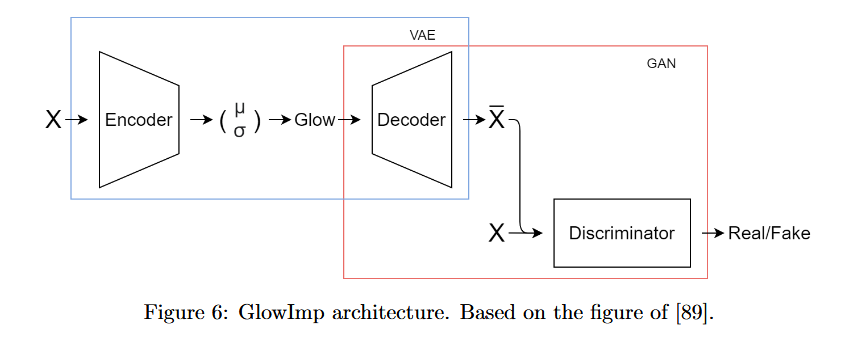
• [90]에서는 Gaussian latent distribution에서 missing data로 인한 편향을 수정하기 위해 shift correction이 사용됨. 이는 hyperparameter λ를 사용해 latent distribution을 중앙으로 정렬함. 이 때 사용되는 VAE는 β-VAE가 사용됨.

6.3 Data Augmentation through GAN

• GAN architecture은 데이터 분포를 직접 복사하지 않고 main feature들을 추출하여 학습을 통해 새로운 데이터를 생성함. 이는 데이터 변환이 아닌 독창적인 새로운 샘플을 합성할 수 있게 해줌. 이를 통해 합성된 데이터의 일반화와 창의성을 높일 수 있음. 또한, GAN은 labeling 되지 않은 데이터가 없는 unsupervised learning에서도 활용 가능함.

6.3.1 Taxonomy for the GAN algorithms reviewed

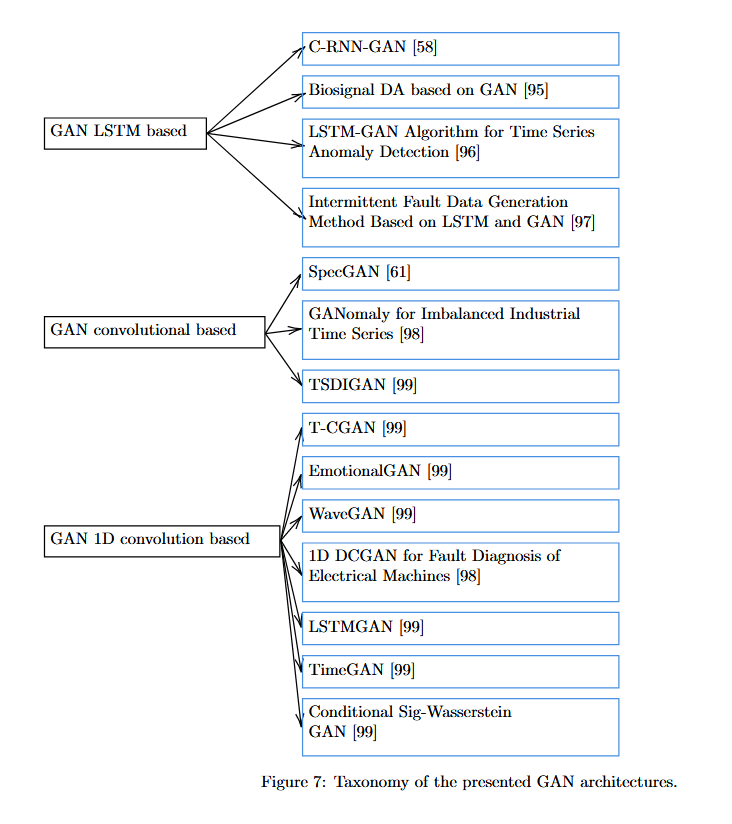
6.3.2 Long-Short Term Memory(LSTM) based GANs

• 시계열 데이터 처리를 위해 fully connected layers와 convolutional layers를 recurrent layers로 대체하여 데이터의 temporal features(시간적 특징)을 연결하는 메모리를 가지도록 함. 이를 통해 입력 데이터가 가지는 시간 정보를 처리 가능.

• C-RNN-GAN[58]: 음악 트랙 학습 및 합성에 사용된 알고리즘으로 LSTM blocks[92]을 주요 학습 구조로 사용함. 학습 알고리즘은 표준 GAN과 동일한데, network genereator는 각 입력을 이전 셀의 출력과 연결하여 학습하고 이 때 discriminator는 양방향 순환 네트워크(bidirectional recurrent network)로 구성됨. 이는 시간적 종속성을 강화함.

• Biosignal DA based on GAN[95]: 시계열 데이터에 적응하기 위해 generator와 discriminator 네트워크 모두에서 LSTM 셀로 구성된 GAN architecture를 사용함. discriminator 출력은 각 layer에서 생성된 출력에 average pooling을 적용하여 생성되며, 전체 데이터 샘플을 generator 네트워크에서 생성되는 샘플 확률에 해당하는 고유한 스칼라 출력으로 평균화함.

• LSTM-GAN Algorithm for Time Series Anomaly Detection[96]: 이상치 탐지에 사용되는 모델로 discriminator에서 LSTM layer를 사용해 시간 정보를 추출하고, GAN은 데이터에서 중요한 feature들을 추출하는 기능을 수행함. 데이터의 이상치를 탐지하기 위한 훈련에는 두 단계가 있는데, 먼저 training phase에서는 표준 GAN에서와 같이 discriminator가 real/synthetic data를 구분하도록 훈련시킴. 다음으로 testing phase에서는 데이터 샘플의 feature들을 추출하고 generator에서 재구성함. discrminator에서 재구성된 데이터와 원본 데이터를 비교하여 이상치를 탐지함.

• Intermittent Fault Data Generation Method Based on LSTM and GAN[97]: GAN architecture를 사용하여 두 가지 다른 유형에서 데이터 시퀀스를 생성함. 각 GAN의 generator와 discriminator는 전압 신호 데이터와 시퀀스 각 단계의 샘플링 길이를 처리하는 many-to-many LSTM 모델로 구성됨. generator 출력은 전압과 길이에 대한 두 개의 벡터로 구성되며, discriminator는 이러한 데이터를 처리하고 출력은 각 단계의 분류를 평균하여 고유한 이진 출력을 생성함.

6.3.3 Convolutional GANs applied to the time series domain

• 시계열 데이터에 GAN을 적용하는 가장 널리 사용되는 방법은 시계열 데이터를 이미지로 변환하여 처리하는 것임. 이는 복잡한 GAN architecture를 설계하는 대신 image 포맷으로의 변환에 초점을 맞추므로 구현이 간단함.

• SpecGAN[61]: 오디오 샘플을 나타내는 spectrogram에서 동작하는 알고리즘. 먼저, fourier transform을 통해 데이터의 frequency matrix를 생성하고 로그 스케일로 변환 및 정규화를 수행한 후 3표준편차로 자르고 [-1,1] 범위에서 크기가 조정됨. 이를 통해 오디오 샘플을 이미지로 변환함. 이러한 이미지에 DCGAN을 적용하여 이미지를 생성한 후 역변환을 통해 오디오 데이터로 복원하여 DA를 수행함.

• GANomaly for Imbalanced Industrial Time Series[98]: 산업 분야에서 이상치를 탐지를 수행하기 위해 제안됨. generator는 encoder-decoder-encoder 네트워크로 구성되어 feature extraction에서 latent representation을 학습함. 이 때, 앞에서와 마찬가지로 시계열 데이터는 spectrogram으로 변환되어 이미지 형태로 처리되었으며, 12~48 kHz로 수집된 베어링 데이터를 사용해 이상치 탐지를 테스트함.

• TSDIGAN[99]: 교통 결측값을 복원하기 위해 제안된 알고리즘. GASF 알고리즘은 데이터를 극좌표로 변환하여 시계열 데이터를 matrix로 변환하는데 이를 통해 시간 종속성을 유지할 수 있음. 이러한 전처리된 데이터는 convolutional-based-GAN을 통해 결측값을 복원함.

6.3.4 1D convolutional GANs

• 1D CNNs는 전통적인 2D CNN의 convolution 연산을 1D로 대체한 구조로 시간 시계열 데이터에서 시간적 종속성을 학습하며, 필터의 차원을 1D로 낮추어 적용함. 이 방법은 기존 GAN architecture를 간단히 시계열 도메인에 적용할 수 있어 유용함.

• T-CGAN[106]: 2D convolution layer를 가지고 있는 Conditional GAN architecture를 1D convolution으로 변환하여 시간 시계열 데이터를 처리함. 모델의 성능은 하나의 synthetic dataset와 3개의 real dataset으로 검증됨.

• EmotionalGAN[108]: 1D convolution layer로 구성된 GAN을 사용하여 ECG 데이터셋을 증강해 SVM 및 random forest 모델을 통한 감정 분류의 성능을 향상시킴.

• WaveGAN[61]: 사운드 데이터 생성을 위한 1D convolution 기반 GAN 모델로, 1D로 변형된 DCGAN를 사용함. 오디오 데이터의 특수성으로 인해, 1D convolution은 이미지 처리의 2D convolution에 비해 더 넓은 receptive field를 가져야 하는데, 따라서 더 넓은 filter를 사용해야 함. 이러한 field의 확대는 1차원을 줄이고, 5x5 convolution에서 25개의 1차원 convolution으로 변경하고, 네트워크의 매개변수 수를 유지함으로써 보상됨.

• 1D DCGAN for Fault Diagnosis of Electrical Machines[109]: DC 신호 증강을 위해 사용된 방법. DCGAN의 기존의 2D convolution을 1D convolution으로 변경하여 적용함. 이 때, 서로 다른 두 개의 GAN을 사용하는데, 하나는 정상 신호를 생성하고 다른 하나는 잘못된 신호를 생성하는 역할을 함.

• LSTMGAN[96]: 1D convolution과 다른 기술을 결합하여 사용함. discriminator network는 LSTM cell을 사용하고, generator는 1D convolutional layers를 사용하여 둘을 결합하여 사용함.

6.3.5 Time series Generative Adversarial Networks (TimeGAN)

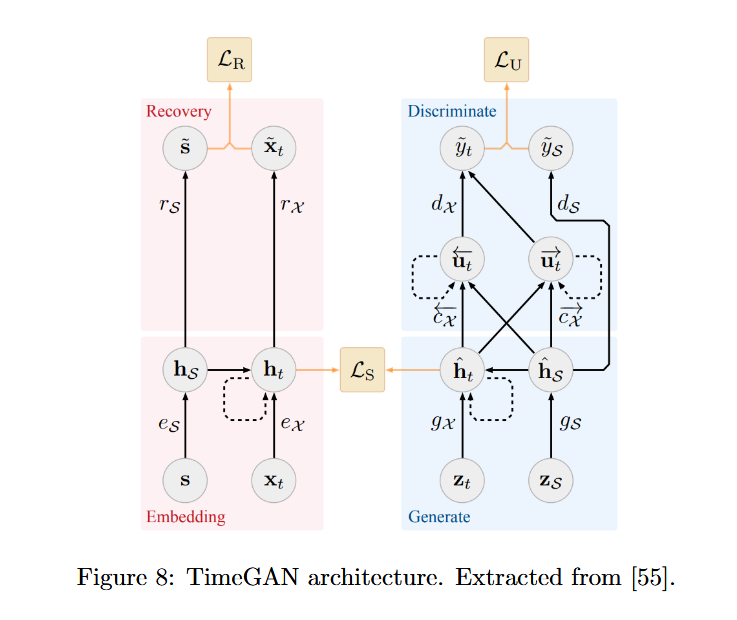
• TimeGAN architecture[55]는 시계열 데이터에 대해 단계적 종속성을 반영하기 위해 새로운 손실 함수를 추가하여 이전의 다른 방법과 차별화를 가짐.

• 데이터를 특징에 따라 static features(S)와 temporal features(X)로 구분하는데, S는 시간에 따라 변하지 않는 features를 의미하고 X는 시간에 따라 변하는 features를 의미함.

• TimeGANs architecture는 generator, discriminator, encoder, recovery networks로 구성됨. 먼저, generator network는 latent space에서 synthetic data를 생성하고 discriminator network는 latent space에서 input을 받아 real/synthetic data를 구별하는 역할을 함. 그리고, encoder와 recovery network는 입력 데이터를 latent space에 임베딩하고 복원하는 역할을 함.

• TimeGAN의 주요 특징은 generator가 데이터의 단계적 종속성을 학습하도록 강제한다는 점임. 이를 위해 generator는 합성 임베딩 hs, ht−1을 입력으로 수신하고 다음 벡터 hs, ht를 계산함. 이 함수는 generator 예측을 실제 데이터와 비교하는 새로운 supervised loss fuction에 의해 학습됨.

• TimeGANs의 objectvies는 다음과 같이 3가지로 구성됨. -Reconstruction loss: encoder와 recovery network의 출력이 원본 데이터를 얼마나 잘 복원하는지 측정하는 함수

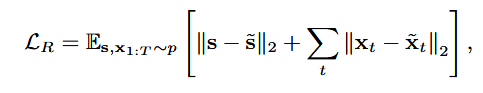
-Unsupervised loss: real/fake sample을 구별하려고 시도하는 일반적인 GAN의 loss fuction와 동일함.

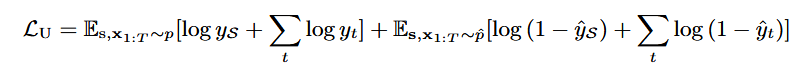
-Supervised loss: generator가 데이터의 conditional transition을 잘 학습하도록 하기 위해서, generator가 생성한 real sample과 synthetic sample 간의 유사성을 측정하도록 설계됨. 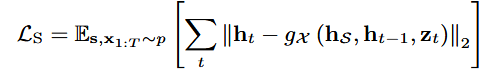이 때, gx는 generator에 의해 합성된 샘플을 나타냄.

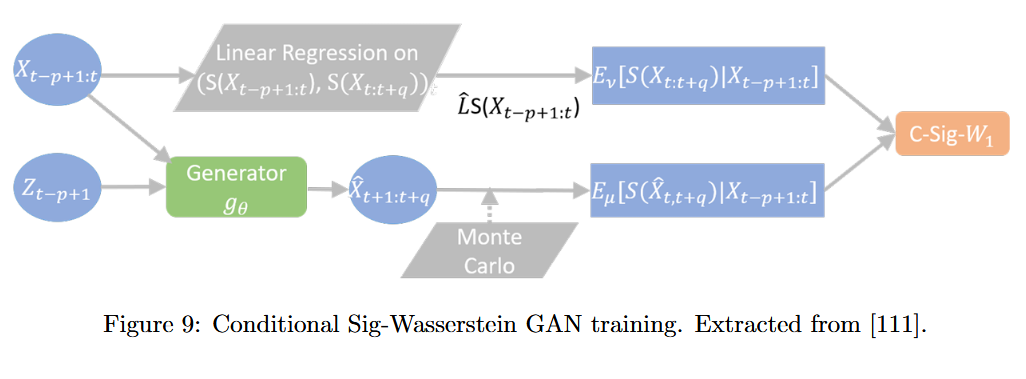
6.3.6 Conditional Sig-Wasserstein GAN

• 시계열 데이터에의 장기적 시간 의존성(long temporal dependencies)을 유지하며 이전 모델과 비교하여 좋은 품질의 synthetic data를 생성하는 방법.

• Wasserstein distance를 기반으로 데이터 경로 공간을 측정하여 discriminator에서 신경망을 사용하는 대신 Linear Regression을 활용함으로써 훈련 과정을 단순화시킬 수 있음. 또한, generator에서는 AR-FNN을 사용하여 시계열 데이터의 시간적 종속성을 캡쳐하여 데이터를 생성시킬 수 있음.

6.4 DA based on Dynamic Time Warping(DTW)

6.4.1 DTW Barycenter Averaging

• DTW는 두 데이터 시퀀스 간의 유사성을 측정하는 고전적인 알고리즘으로 DA에 활용되어 새로운 synthetic sample을 생성함.

• DTW averaging은 데이터 분포를 조작하여 무한한 새로운 샘플을 생성하여 시계열 데이터의 분류 성능을 향상시키고자 함. 이는 가중치를 변화시키는 방법으로 수행됨. 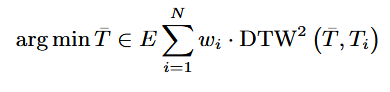샘플 집합 D = {(T1, w1) , . . . , (TN , wn)}는 공간 E에 임베딩되고 w는 각 샘플의 가중치를 의미함. 이 때, 평균 T는 Expectation-Maximization algorithm을 사용해 계산함.

• 가중치 결정 방법은 다음과 같음. Average All: 모든 샘플에 균일한 Dirichlet distribution을 사용해 가중치를 생성하는 방법으로 잘못된 공간에 데이터를 채울 가능성이 있다는 단점이 존재함. Average Selected: 근접한 샘플들의 하위 집합을 선택하여 가중치를 생성하는 방법으로 샘플의 하위집합이 서로 가까이 있기 때문에 데이터의 불필요한 공간에 데이터를 채우는 것을 방지할 수 있음. Average Selected with Distance: average selected 방식과 같이 하위 집합을 선택하고 선택된 근접 샘플 간 상대적 거리를 계산해 가중치를 조정하는 방법.

6.4.2 Suboptimal element alignment averaging

• DTW 알고리즘을 기반으로 한 DA 기법으로 다차원 신호 간의 warping path W를 계산하여 새로운 시계열을 생성하는 기법.

• 먼저, DTW 알고리즘을 사용하여 두 입력 신호 X1, X2의 warping path를 계산하여 거리를 최소화함. 다음으로, (0,1)에서 uniformly distributed random number를 삽입하여 새로운 warping path를 만들고 매개변수를 활용해 두 경로를 정렬함. 그리고, 최적화된 경로를 연결하여 새로운 경로를 생성한 후 이 경로로부터 새로운 시계열 신호를 생성함. 이렇게 생성된 시계열 신호에 정규분포를 따르는 random variance를 추가하여 DA를 수행함.

• 이 기법은 DTW 대신 텍스트 또는 이미지 데이터에 적합한 정렬 기법이 사용될 수도 있으며 정렬 방법만 변경하여 다른 데이터 유형에도 쉽게 적용이 가능함.

7. Discussion

• 시계열 데이터 증강은 데이터셋 품질 개선에 필수적이며, 데이터 생성의 어려움을 완화해줌. 일반적으로 이 작업에 제시된 기법들은 대부분 시계열에 특화되어 설계된 알고리즘들이지만, 일부는 이미지 처리와 같은 다른 영역에서 시작된 구조를 시계열 데이터에 맞게 수정하여 적용됨.

• 알고리즘은 다양한 크기와 유형의 데이터셋을 처리 가능함. 특히, 인공지는 알고리즘은 특정 데이터를 기반으로 학습하기 때문에 거의 모든 데이터 소스에서 작동이 가능함. 이로 인해 대부분의 알고리즘이 사용하는 시계열 window의 크기가 달라질 수 있음.

7.1 Advantages

• Traditional algorithms: 기존에 존재하는 예제를 수정하여 작업함으로써 variation을 통제할 수 있음. 또한, hyperparmeter 수가 적어 알고리즘이 비교적 간단해짐으로써 설정 시간이 짧고 학습에 필요한 데이터 요구량이 적음.

• VAE: 원본 데이터셋의 latent distribution에서의 표준편차를 조작하여 생성되는 데이터의 변동성을 정밀하게 제어 가능함. 이는 이상치 탐지에서 우수한 성능을 나타내어 자주 사용됨.

• GANs: 원본 데이터셋의 분포를 학습하여 원본 데이터셋과 유사한 합성 데이터셋을 생성하고, 이를 통해 뛰어난 일반화 성능을 가짐. 또한, 최신 알고리즘으로서 학계의 주목으로 인해 지속적으로 성능 향상에 관한 연구가 진행되고 있음.

7.2 Disadvantages

• Traditional algorithms: 기존 데이터셋의 요소를 변형하는 방식으로 작동하기 낮은 품질의 데이터를 생성하거나 새로운 데이터를 생성하지 못함. 앞에서 검토된 알고리즘에서는 입력 데이터를 정규화하기 위해 전처리 단계가 필요하며, 이는 더 복잡한 알고리즘이 발생 가능함.

• VAE: GAN과 같은 최신 생성 모델보다 생성 가능한 데이터 수가 적음. 하지만, 생성된 데이터의 변동성을 정밀하게 제어할 수 있어 특정 분야에서는 계속해서 사용됨.

• GANs: 현재 사용 가능한 가장 복잡한 모델 중 하나로, 훈련이 어렵고 결과를 얻는 것이 어려움. 주요 문제로는 Mode Collapse, instability, convergence evaluation, evaluation metrics와 같은 문제가 존재하고, 이러한 문제들로 인해 데이터의 신뢰성이 부족해짐.

7.3 Open issues and challenges

• Traditional algotithms은 기존 데이터를 변형하여 데이터를 증강하기 때문에 생성된 데이터가 제어력이 강하지만 다양성이 부족한 문제가 존재함. 이에 반해, data generation algorithms은 원본 데이터와 비교적 무관하게 새로운 데이터를 생성할 수 있지만, 지나치게 공격적인 생성으로 인해 품질이 저하되는 경우가 존재함.

• Traditional alogorithms은 훈련된 모델을 다른 문제에 적용하기 어려움이 있는 데에 반해, VAE는 NN을 사용함으로써 동일한 훈련된 모델을 다양한 문제에 적용할 수 있어 더 유연함을 가짐.

• GANs은 Nash equilibria, Mode collapse, Gradient vanishing, instability와 같은 문제로 인해 모델을 최적화하는 과정이 매우 복잡하고 어려움.

• 모든 생성형 모델은 각각의 evaluation metrics을 가짐에도 불구하고, 일관된 metric에 대한 합의가 부족함. 추가적으로, GAN model에서는 훈련 과정에서 정지 조건에 대한 명확한 정의가 내려지지 않은 문제도 존재함.

3. Conclusion

• 데이터 증강(DA)은 최근 급격히 발전하며 다양한 분야에 적용 가능성이 확대되고 있다. 이 논문은 시계열 데이터 증강을 위한 전통적 알고리즘, VAE, GAN 기반 접근법을 분류 체계로 정리하고, 각 알고리즘의 대표적인 방법을 비교 및 분석하였다. 이를 통해 저자는 각 알고리즘의 장단점과 응용 분야를 조명하며 향후 연구 방향을 제시한다.

4. Take away

• 데이터 증강의 중요성
• 데이터 증강에 사용되는 주요 알고리즘 분류
• 데이터 증강에 사용되는 각각의 알고리즘의 구현 원리 및 사례
• 최신 데이터 증강 기술의 한계와 향후 과제